Random testing, in isolation, is a stupid idea. You take a program, which has a practically infinite amount of possible inputs, you randomly pick one of those infinite possibilities in the hopes of breaking the program, or some assertion about the program, and it actually works (discovers bug) in even the most naive form possible, which is essentially the following loop:

while True:
    input = generate_random_input()
    if not property(input):
        report_bug(input)

Over the years, people have developed many different improvements on this naive form I described. The most famous example is coverage guidance, which led to the rise of fuzz testing in the last decade, finding thousands, perhaps millions of different bugs across systems. In coverage guiding, the random inputs are biased towards inputs that increase the code coverage of the system under test, leading to better exploration of the input space. The modified loop looks like this:

pool = initialize_pool()
while True:
    input = mutate(select_from_pool(pool))

    if not property(input):
        report_bug(input)

    if increases_coverage(input, pool):
        pool.add(input)

As we found more and more bugs, it became more and more apparent that finding bugs was, and is, not sufficient. Someone must validate and fix the said bugs. Hence, the "counterexamples", inputs that trigger the alleged bugs, must be legible, inspectable, managable. Ideally, the tester should receive the simplest possible form of the input, isolated from any noise, only providing the minimal necessary structure for the reproduction, and the eventual fixing, of the bug. The solution emerged in different names, but in similar shapes, minimization, delta-debugging, or shrinking.

Shrinking is one of these ideas that immediately make sense once you hear about it. Let's say that we generated some random input for some program, perhaps a random PNG image for an image processor. Once a bug is triggered in some part of the system, we would like to get the simplest PNG possible that retriggers the input. For this, we can designate some simplification procedures. We can dim each pixel independently, making the picture darker, turning as much of the pixels as possible into #000000. We can also remove some parts of the image completely by cropping the image. As it turns out, many times these simplifications are equivalent to making the values smaller, such as reducing the size of the image, or converging pixels to white as the smallest hex coded color, hence the name shrinking. In shrinking, we start from a bug-triggering input case, and we repeatedly produce smaller (shrunk) versions of the input as long as there is a smaller input that still retriggers the bug. If we cannot find a smaller instance, we report the original input to the user.

Given some input I that triggers a bug, we can define a shrinking function shrink(I) -> [I_1, I_2...I_n], we can write a version of the shrinking algorithm as follows:

def shrink_input(input):
    for smaller_input in shrink(input):
        if triggers_bug(smaller_input):
            return shrink_input(smaller_input)
    return input

Enters temporality. The default perspective into random testing is that it produces many inputs from scratch, you may conjure up PNGs from thin air, produce balanced binary trees, generate network topologies, create virtual physical environments or write texts with grammatical faults, all depending on your domain. However, there are many systems where generating inputs from scratch is not an option, you cannot first generate an entire well-formed SQLite database from scratch, and then a SQL query over the database, only to test the result of a simple query. Therefore, instead of trying to generate such complex structures from scratch, random testing have mostly converged to using stateful generation. In stateful generation, we add a notion of time to random testing. We start from an initial state S_0 at time t=0, and generate an interaction against a system based on its API. For a SQL database, these can be SQL statements, for a key-value store, these are insert, delete, get...

After every interaction, the state of the system possibly changes, affecting the next input we generate. Assuming we're lucky (the system itself is not affected by the physical time), every action will be another tick, going from t=0,1,2...n until we discover a bug. We already know the logical next step, shrinking, but how do we shrink these actions that have these potential linear dependencies with each other, every action possibly depending on all prior actions to be valid? Below is an example of such a dependency chain:

CREATE TABLE t0 (c0, c1);
INSERT INTO t0 VALUES (0, 0), (1, 1), (2, 2);
SELECT FROM t0 WHERE c0 >= 1; -- @bind r
-- @assert r = (1, 1), (2, 2)

The language depicted here is a small augmentation of SQL for binding results of intermediate queries and asserting facts about them, this specific example highlights a containment assertion, we expect to find the values we inserted when we search for them. If we go about removing parts of this structure, similar to what we did for PNGs in the stateless instances, it is possible that we render the test invalid. If you remove the first line (CREATE TABLE...), you expect that all the following interactions fail, hence the assertion will fail, but the test itself will be invalid.

There are some solutions to this scenario, the first of which is to restrict the shrinking by slicing the input we have at hand. Take the following alternative sequence of interactions:

CREATE TABLE t0 (c0, c1);
CREATE TABLE t1 (c0, c1, c2); -- (2)
INSERT INTO t0 VALUES (0, 0), (1, 1), (2, 2);
INSERT INTO t1 VALUES (NULL, 'why', 'not'); -- (4)
SELECT FROM t1 WHERE c0 != 1 OR c1 != 'how'; -- (5)
SELECT FROM t0 WHERE TRUE; -- (6)
SELECT FROM t0 WHERE c0 >= 1; -- @bind r
-- @assert r = (1, 1), (2, 2)

We can slice this program up into 2 parts, the parts that are relevant to the failure, and the parts that are irrelevant. This relevancy is of course a heuristic, perhaps what seems irrelevant is the cause of a failure we see, hence we need to make sure our assumptions are sound. The slicing heuristic I'll use is table-based slicing, where we only care about the interactions with the tables related to the failing assertion. r is computed by a query over t0, hence we remove all interactions that do not read or write to t0. In the example above, this slicing allows us to eliminate queries (2), (4), and (5) as they do not mention t0, but rather only t1. Another heuristic is to remove as many reads as possible, as they (hopefully) do not affect the state of the database, which allows us to remove query (6) as well. After slicing, we are left with the original example, which is much smaller.

We can, however, have another type of shrinking, one that leverages the temporal generation instead of trying to work through the limitations it imposes. What do we do, we time travel!

Instead of starting shrinking from the large structure that triggered the bug, we start from the random seed that produced the structure in the first place. We start generating the input at t=0, but at some point in time t=j, we manipulate our decision, we generate a smaller input. It must be noted that every single action we take after t=j is now possibly changed, because we went back in time and changed the past, affecting every future decision from that point on. The good thing about this approach is that we preserve the original invariants that the generator respected, because we did no actual shrinking, we only manipulated the generation process into generating a smaller structure.

The first approach of going from a large structure to smaller ones by using a reproducer for detecting if the fault continues to occur is typically called external or type-based shrinking, although I like to call it structural shrinking. The second approach is called internal, or integrated shrinking; Property-Based Testing libraries are typically divided in the ways they pick the shrinking methodology, Hypothesis famously uses integrated shrinking, whereas many of the QuickCheck descendents use structural shrinking.

Fast forward to DST. The discussion of integrated vs structural shrinking is a long one, one which I'll not take sides at the moment; but there's a special flavor of random testing that structural shrinking is not really an option, deterministic simulation testing. I won't go into the very specific details of DST in this post, I think there's already some great resources such as Phil's blog post that are sufficient for it. In short, DST is what you need when testing systems where you are not lucky enough that you can remove the notion of time from your system, violating the assumption of the previous section. Many times, especially in distributed systems or concurrent programs, physical time is an important part of how your system works, and you cannot abstract over it, you need to work with the physical time. In such cases, you cannot naively shrink your inputs, because you cannot even reproduce them most of the time. When testing a time-aware system, running the same sequence of interactions twice doesn't guarantee the same outputs or results, let alone preserving the error if you change them.

In DST, the execution layer is perfectly deterministic, meaning that physical time and effects are abstracted from the system, so your tests are perfectly reproducible, and that's a great thing, because it gives you the ability to debug previously undebuggable bugs as you can reproduce the same exact sequence of interactions, solving the infamous pain of Heisenbugs, but does it? The central issue with perfect reproducibility is that you cannot change anything in the system because of the temporality. You can go back in time, but you cannot change anything, you can only observe. The moment you change something, every next decision is out of your control, so you cannot know the exact affects of your change. Did you actually fix the bug, or did the scheduler just make a different choice that removed the bug?

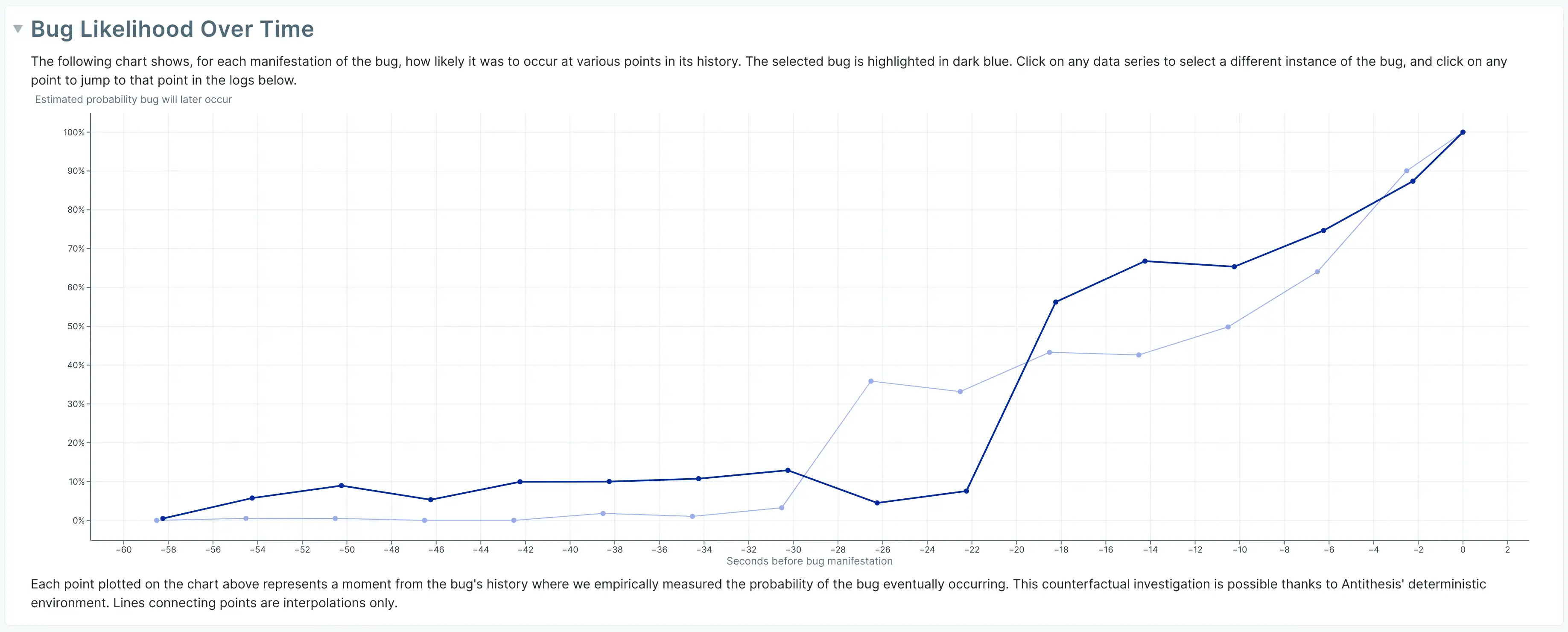
Engineers at Antithesis, the company pioneering DST at the moment, have found a very cool method for overcoming this problem, which I like to call temporal shrinking, or rather temporal fault localization. The idea is as follows:

You have a temporal test, some sequence of inputs spanning some amount of time. As I said, you can change any decision at any point in time, which will affect possibly everything from that point on. Let's assume that some decisions at arbitrary points in time j_0, j_1...j_k are the triggering conditions of the bug. If you change anything after t=j_k, the reproduction of the bug must not change, so all 100% of the decisions after j_k must be irrelevant. So, we can pick random points in time, change the decisions at such points, and check how they affect the percentage of bugs found afterwards. In a very rare bug, namely one that only reproduces under conditions j_0...j_k, if you change any of the j_0...j_k, you would get a 0% retrigger rate.

This core idea of retrigger percentage allows Antithesis to localize the bug temporally, identifying key pieces in time that are crucial to the retriggering of the bug, which is ultimately a form of shrinking, hence the name of the article. It also feels somewhat descendent of the spectrum based fault localization techniques that identify differences between positive and negative inputs, but moving it into the temporal realm.

A potential analysis built on this capability leads to the following bug probability graph shown below. The exact details of the computation for producing the graph can be found in Antithesis docs, as well as how to interpret the results of the graph.

It should be noted that I'm not affiliated with Antithesis (although I collaborate with them on different topics), and temporal shrinking is not limited to Antithesis, but rather applicable for any Deterministic Simulation Environment. I posit that in a few years, we will probably see similar tools built on concurrency testing libraries such as Shuttle or Fray, because they are in a similar design space and have the same challenges with respect to shrinking and debugging.