Learner’s Guide to Functional Programming#1: Implementing Lists in JavaScript

Although this article was written first, I suggest you read the prequel I read as background. Leaving the link below.

There are many articles introducing functional programming. They mention immutability, first class functions, purity, recursion, and many other concepts with usually small examples of each one of them. In this series, I want to try a different way. We will implement functional data structures within using a very minimal subset of Javascript. No loops, no mutable variables, no builtins except primitive types.

The first of these data structures is a list. A list is a very simple data structure, below is a simple definition of a list type in typescript.

type List = { variant: "nil" } | { variant: "cons", elem: any, rest: List }

Here, we either have a “nil” variant with no elements, and a “cons” variant with a en element, as well as the rest of the list. Before going into implementation details, let’s imagine how would such a list look like.

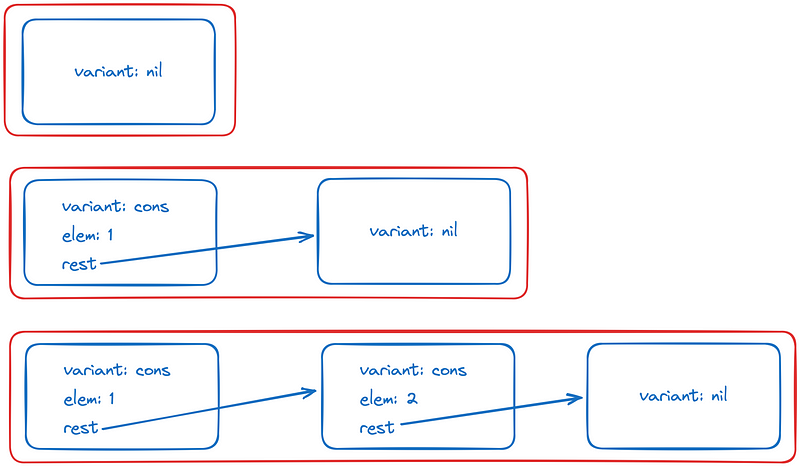
Below are the same definitions in Javascript code.

const emptyList = { variant: "nil" }; \\ []
const singleElemList = { variant: "cons", elem: 2, rest: emptyList } \\ [1]
const twoElemList = {
  { variant: "cons", elem: 1,
  rest: { variant: "cons", elem: 2, 
  rest: emptyList }
} // [1, 2]

We start from the first element with a variant: "cons" node, end we denote the end with a variant: "nil" node.

Here, we will have two constructors, one per variant.

const mkEmpty = () => (
    {
        variant: "nil"
    }
)

const mkList = (elem, rest) => (
    {
        variant: "cons",
        elem: elem,
        rest: rest
    }
)

If we want to make a list of only one item, we could easily compose them.

const mkListFromElem = (elem) => (
    mkList(elem, mkEmpty())
)

Implementing accessors is pretty straightforward.

const isEmpty = (list) => (
    list.variant === "nil"
)


// Below, we introduce the list notation. ":" is the prepending operation.
// (elem : rest) -> elem
// Get first element
const head = (list) => (
    list.elem
)

// Get the rest of the list
// (elem : rest) -> rest
const tail = (list) => (
    list.rest
)

As we now have the basic building blocks at hand, we can start defining more complicated functions. The first is the length function.

// length(elem:rest) = 1 + length(rest)
const length = (list) => (
    isEmpty(list) ? 0 : 1 + length(tail(list))
)

The definition goes, is you have an empty list, that list has 0 length. For any other list, you can add one to the length of the rest of the list and return that.

length(list) = length([list.head]) + length([list.rest]) is the relation we are using for this function.

Although we could continue implementing functions in ad hoc manners, now I will introduce you with Higher Order Functions map, filter and reduce. We will then use these functions as building blocks of more complex functions.

const map = (list, f) => (
    isEmpty(list) ? mkEmpty() : mkList(f(head(list)), map(tail(list), f))
)

Map function applies a function f to all elements of a list. You can see that we are effectively recreating the list by computing f on head(list) and passing it to the map(tail(list), f) .

const filter = (list, p) => (
    isEmpty(list) ?
        mkEmpty()
        : f(head(list)) ?
            mkList(head(list), filter(tail(list), p))
            : filter(tail(list), p)
)

Filter takes a list, and a predicate p , a predicate is a type of function that returns a boolean. Filters create a list with the elements passing the predicate.

const reduce = (list, f, acc) => (
    isEmpty(list) ? acc : reduce(tail(list), f, f(acc, head(list)))
)

Reduce is the last one of our building blocks. We use reduce to apply functions over the list by propagating the result. I usually find reduce the most confusing among these three, so let’s use reduce for some functions in order to allow a more comprehensive understanding.

// Instead of recursively calling tail ourselves, we call reduce
// with the initial value of 0, incremented for every node.
const lenReduce = (list, f) => (
    reduce(list, (acc, elem) => acc + 1, 0)
)

// Reverse initiates an empty list. At every point, we take the
// head, prepend it to the accumulator.
const reverse = (list) => (
    reduce(list, (acc, elem) => mkList(elem, acc), mkEmpty())
)

Another important building block is concat which allows us two concatenate two lists.

// We will use ++ for concat notation.
// concat(l1, l2) = l1 ++ l2

// If the first list is empty, we can just return the second list.
// Otherwise, we concatenate the rest of the list with and prepend
// the first element of the first list.
const concat = (list1, list2) => (
    isEmpty(list1) ? 
        list2 
        : mkList(head(list1), concat(tail(list1), list2))
)

As we have concat we can now define prepend and append.

// prepend(list, elem) = (elem : list)
const prepend = (list, elem) => (
    mkList(elem, list)
)

// append(list, elem) = list ++ [elem]
const append = (list, elem) => (
    concat(list, mkListFromElem(elem))
)

As you see, prepend is the same as mkList and append is equivalent to creating a one element list and concatenating it to the end.

The last function we are implementing is the indexing function. Here, we pass the index parameter n and we decrease it as we move within the list.

// nth((elem:rest), n) = nth(rest, n - 1)
const nth = (list, n) => (
    n === 0 ? head(list) : nth(tail(list), n - 1)
)

Below is the Github repository for the functions introduced within this article.