Learner’s Guide to Dynamic Programming#2
Dynamic programming is an algorithmic problem solving paradigm focused on recognization and elimination of repetitive computation. Earlier this week, I had another article introducing dynamic programming and a perspective I found useful. I’m leaving a link for that below.
Dynamic programming is an algorithmic problem solving paradigm focused on recognization and elimination of repetitive… medium.com
In this second article, I will focus on a different example, Wildcard Matching.
Problem Statement
Given an input string (
s
) and a pattern (
p
), implement wildcard pattern matching with support for
'?'
and
'*'
where:
-
'?'Matches any single character. -
'*'Matches any sequence of characters (including the empty sequence).
The matching should cover the entire input string (not partial).
Solution
Again, we should start with small examples.
isMatch(“”, “”) = True => Empty pattern matches empty string.
isMatch(“”, “a”) = False => A letter pattern cannot match empty string.
isMatch(“”, “?”) = False => A single matcher pattern cannot match empty string.
isMatch(“”, “*”) = True => A wildcard matcher pattern can match empty string.
isMatch(“a”, “”) = False => Empty pattern cannot match a non-empty string.
So, we are actually finished with small examples. As I will show you in a minute, we can reduce any pattern to these patterns by recognizing a set of simple relations.
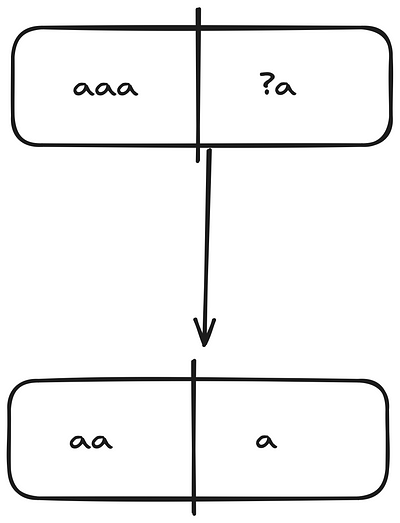
isMatch(“a__”, “a__”) or isMatch(“a__”, “?__”) = isMatch(“__”, “__”) => When a letter pattern or a single matcher matches the first character of the string, we can consume both characters and control the rest of S and P.
This last one is the real deal. What happens when we meet a wildcard pattern?
isMatch(“a__”, “*__”) has 3 possibilities.
- “*” matches exactly one character. So, both characters are consumed.
isMatch(“a__”, “*__”) = isMatch(“__”, “__”)
2. “*” matches zero characters. So, only “*” is consumed.
isMatch(“a__”, “*__”) = isMatch(“a__”, “__”)
3. “*” matches one or more characters. So, only “a” is consumed.
isMatch(“a__”, “*__”) = isMatch(“__”, “*__”)
Let’s put a visual representation.
Below is the matcher tree for “aaa” and “*?a”.
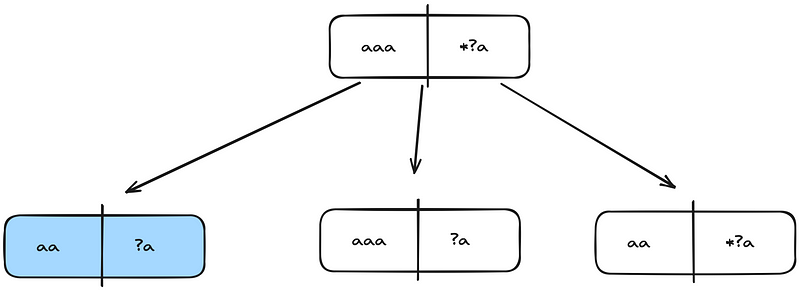
Respectively, below are the matcher trees for these 3 child nodes.

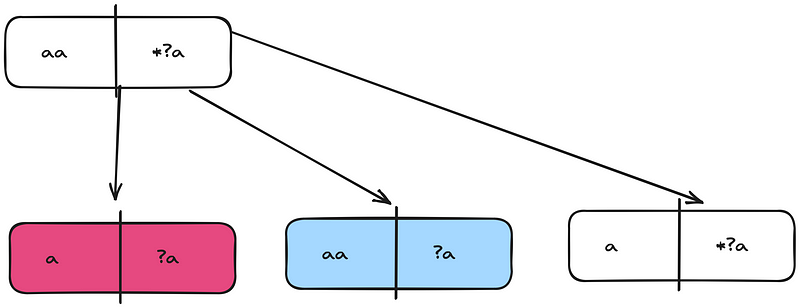
You should now realize that I started coloring the nodes that appear more than once in distinct colors. So, even at this second step, we have a duplicate node, the blue isMatch(aa, ?a).
At this point, the visual representation allows us to reach a similar conclusion even within this picture. Each “*” leads to an exponential growth in the number of computational steps, as it creates 3 separate branches.
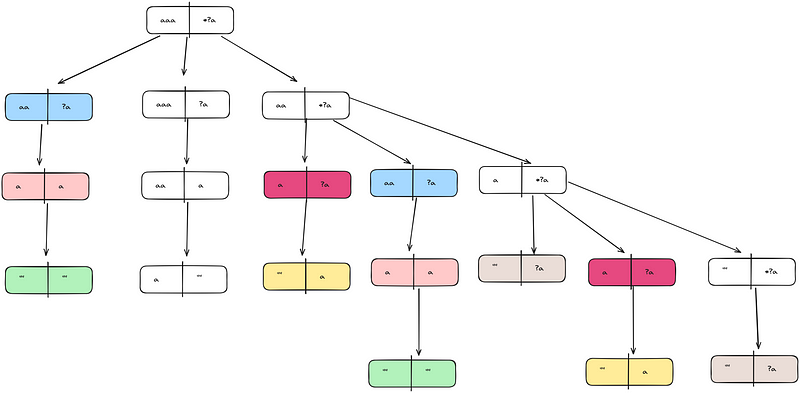
The green nodes are the isMatch(“”, “”) nodes, reaching such a node means that we actually reached a match.
Even within this small example with only one “*” node, we can see 5 duplicates. So, can we actually compute the number of steps? In the general case, probably no. I’ll give you the numbers for a specific set of cases though.
Let’s examine isMatch(a…a, *…*) for different lengths of “a” and “*”. Below, I have written two numbers, the first one is the number of calls to isMatch(“”, “”) , and the second is the number of all function calls for that query.
isMatch(a, *): 2, 5
isMatch(a, **): 4, 11
isMatch(a, ***): 6, 19
isMatch(a, ****): 8, 29
isMatch(a, *****): 10, 41
isMatch(aa, *): 2, 8
isMatch(aa, **): 8, 25
isMatch(aa, ***): 18, 56
isMatch(aa, ****): 32, 105
isMatch(aa, *****): 50, 176
isMatch(aaa, *): 2, 11
isMatch(aaa, **): 12, 45
isMatch(aaa, ***): 38, 127
isMatch(aaa, ****): 88, 289
isMatch(aaa, *****): 170, 571
isMatch(aaaa, *): 2, 14
isMatch(aaaa, **): 16, 71
isMatch(aaaa, ***): 66, 244
isMatch(aaaa, ****): 192, 661
isMatch(aaaa, *****): 450, 1522
isMatch(aaaaa, *): 2, 17
isMatch(aaaaa, **): 20, 103
isMatch(aaaaa, ***): 102, 419
isMatch(aaaaa, ****): 360, 1325
isMatch(aaaaa, *****): 1002, 3509
Some big examples(these do not have the total number)
isMatch(aaaaaaaaaa, **********): 4780008
isMatch(aaaaaaaaaa, ***********): 11414898
isMatch(aaaaaaaaaa, ************): 25534368
isMatch(aaaaaaaaaa, *************): 53972178
isMatch(aaaaaaaaaa, **************): 108568488
isMatch(aaaaaaaaaaa, **********): 10377180
isMatch(aaaaaaaaaaa, ***********): 26572086
isMatch(aaaaaaaaaaa, ************): 63521352
isMatch(aaaaaaaaaaa, *************): 143027898
isMatch(aaaaaaaaaaa, **************): 305568564
isMatch(aaaaaaaaaaaa, **********): 21278640
isMatch(aaaaaaaaaaaa, ***********): 58227906
isMatch(aaaaaaaaaaaa, ************): 148321344
isMatch(aaaaaaaaaaaa, *************): 354870594
isMatch(aaaaaaaaaaaa, **************): 803467056
isMatch(aaaaaaaaaaaaa, **********): 41517060
isMatch(aaaaaaaaaaaaa, ***********): 121023606
isMatch(aaaaaaaaaaaaa, ************): 327572856
isMatch(aaaaaaaaaaaaa, *************): 830764794
isMatch(aaaaaaaaaaaaa, **************): 1989102444
I have tried to uncover some deep function running in the back, but I wasn’t able to find any mathematical equations. If anyone is, I would love to hear your results. But it is clear that length has a multiplicative effect and quickly gets very large.
Of course, this number by itself is not very meaningful as isMatch(“”, “”) is actually cheaper than the memoization call, but I think it gives an intuition on the number of duplicate computations. So, how do we memorize this? I have implemented a very simple cache in the code below.
# Call counter for the measurements in this articc
call_counts = {}
# Call cacher
calls = {}
def isMatch(s: str, p: str) -> bool:
## Caching Parts
# Call counter
if (s, p) in call_counts:
call_counts[(s, p)] += 1
else:
call_counts[(s, p)] = 1
# Memoization
if (s, p) in calls:
return calls[(s, p)]
## Base cases
# When both are consumed, it's a match
if len(s) == 0 and len(p) == 0:
calls[(s, p)] = True
return True
# When pattern is consumed, it's not a match
if len(p) == 0:
calls[(s, p)] = False
return False
# When string is consumed, it's a match if the rest of the pattern is all '*'
if len(s) == 0:
return p[0] == '*' and isMatch(s, p[1:])
## Recursive cases
# Consume both if they match
# a___ <> a___
if s[0] == p[0]:
return isMatch(s[1:], p[1:])
# Consume both if pattern is '?'
# a___ <> ?___
if p[0] == '?':
return isMatch(s[1:], p[1:])
# There are 3 cases for '*'
# a___ <> *___
if p[0] == '*':
# 1. Consume both: so that '*' matches 1 character
c1 = isMatch(s[1:], p[1:])
# 2. Consume string, but not pattern: so that '*' matches 1 or more characters
c2 = isMatch(s[1:], p)
# 3. Consume pattern, but not string: so that '*' matches 0 characters
c3 = isMatch(s, p[1:])
return c1 or c2 or c3
calls[(s, p)] = False
return False
print(isMatch('aa', 'a')) # False
print(isMatch('aa', '*')) # True
print(isMatch('cb', '?a')) # False
print(isMatch('adceb', '*a*b')) # True
print(isMatch('acdcb', 'a*c?b')) # False
print(isMatch('adceb', '*a*b*')) # True
This memoization is kind of hacky, in the sense that you would not able to copy-paste this code into leetcode, but it’s certainly adaptable. Instead of using the strings for the cacher, it’s easy to use the indexes, which in turn means you don’t actually need a map, but rather just a simple 2d array that allows O(1)(constant) indexing.
Conclusion
I like this problem better than the 3sum problem in the first article, as it allows a much more principled way of memoization. The fact that 3sum depended on calls to 2sum was a bit crude and maybe harder to internalize. But isMatch depending entirely on itself allows one to see the call tree much better. If you have any other problems you want solved in different articles, let me know!